13 Lösungen Übungsaufgaben
13.1 Aufgabe 1
13.1.1 Output 1
Lösung: tau paralleles Modell
- alle Ladungen auf 1
- Alle Intercepts der manifesten auf 0
- Alle Fehlervarianzen der manifesten identisch
Modell passt nicht
13.1.2 Output 2
Lösung: essentiell tau äquivalent
- alle Ladungen auf 1
- unterschiedliche Mittelwerte der manifesten Variablen
- Mittelwert von eta auf 0
- unterschiedliche Fehlervarianzen der manifesten Variablen
Modell passt nicht richtig (laut RMSEA und Chi quadrat), CFI und TLI sprechen ganz knapp für Modellfit
13.1.3 Output 3
Lösung: essentiell tau äquivalent
- alle Ladungen auf 1
- unterschiedliche Mittelwerte der manifesten Variablen
- Mittelwert von eta auf 0
- unterschiedliche Fehlervarianzen der manifesten Variablen
Modell passt richtig (CFI, TLI und Chi quadrat), Nur RMSEA spricht knapp gegen einen Modellfit
13.1.4 Output 4
Lösung: tau kongenerisch
- alle Ladungen frei geschätzt
- unterschiedliche Mittelwerte der manifesten Variablen
- Mittelwert von eta auf 0 und varianz von eta auf 1 (Normierung)
- unterschiedliche Fehlervarianzen der manifesten Variablen
Modell passt nicht (alle vier Fitindices sprechen stark gegen einen Modellfit)
13.1.5 Output 5
Lösung: tau kongenerisch
- alle Ladungen frei geschätzt, la11 = 1 (Normierung)
- unterschiedliche Mittelwerte der manifesten Variablen, la10 = 0 (Normierung)
- Mittelwert und Varianz von eta frei geschätzt
- unterschiedliche Fehlervarianzen der manifesten Variablen
Modell passt gut (alle vier Fitindices sprechen stark für einen Modellfit)
13.2 Aufgabe 2
13.2.1 Output 1
# Lösung: vervollständigter Output (tau paralleles Modell)
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta =~
y1 1.000
y2 1.000
y3 1.000
y4 1.000
y5 1.000
y6 1.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
eta 0.317 0.056 5.651 0.000
.y1 0.000
.y2 0.000
.y3 0.000
.y4 0.000
.y5 0.000
.y6 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
eta (veta) 0.824 0.077 10.694 0.000
.y1 (veps) 0.709 0.026 27.386 0.000
.y2 (veps) 0.709 0.026 27.386 0.000
.y3 (veps) 0.709 0.026 27.386 0.000
.y4 (veps) 0.709 0.026 27.386 0.000
.y5 (veps) 0.709 0.026 27.386 0.000
.y6 (veps) 0.709 0.026 27.386 0.000 13.2.2 Output 2
# Lösung: vervollständigter Output (essentiell tau äquivalent, Normierung E(eta)=0)
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta =~
y1 1.000
y2 1.000
y3 1.000
y4 1.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
eta 0.000
.y1 15.205 0.161 94.715 0.000
.y2 14.990 0.164 91.229 0.000
.y3 15.130 0.161 93.897 0.000
.y4 15.070 0.164 92.155 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
eta (veta) 4.125 0.441 9.347 0.000
.y1 (vps1) 1.029 0.141 7.309 0.000
.y2 (vps2) 1.275 0.163 7.837 0.000
.y3 (vps3) 1.068 0.144 7.407 0.000
.y4 (vps4) 1.223 0.158 7.744 0.000 13.2.3 Output 3
# Lösung: vervollständigter Output (tau kongenerisch, Normierung la10 = 0, la11 = 1)
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta =~
item_1 (la11) 1.000
item_2 (la21) 0.749 0.053 14.034 0.000
item_3 (la31) 1.203 0.055 22.016 0.000
item_4 (la41) 0.843 0.046 18.275 0.000
item_5 (la51) 0.692 0.053 12.965 0.000
item_6 (la61) 0.662 0.051 12.899 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
eta 2.563 0.053 48.247 0.000
.item_1 (la10) 0.000
.item_2 (la20) 0.395 0.145 2.723 0.006
.item_3 (la30) -0.823 0.147 -5.583 0.000
.item_4 (la40) 0.786 0.125 6.280 0.000
.item_5 (la50) -0.193 0.145 -1.327 0.185
.item_6 (la60) 0.765 0.139 5.482 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
eta (veta) 0.940 0.088 10.657 0.000
.item_1 (vps1) 0.468 0.040 11.758 0.000
.item_2 (vps2) 0.895 0.061 14.684 0.000
.item_3 (vps3) 0.368 0.043 8.630 0.000
.item_4 (vps4) 0.507 0.038 13.231 0.000
.item_5 (vps5) 0.940 0.063 14.896 0.000
.item_6 (vps6) 0.871 0.058 14.908 0.000 13.3 Aufgabe 3
# Lösung: vollständig beschrifteter Output
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta =~
y1 (la11) 1.690 0.116 14.572 0.000
y2 (la21) 1.943 0.136 14.291 0.000
y3 (la31) 1.905 0.147 13.002 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
eta 0.000
.y1 (la10) 0.245 0.137 1.786 0.074
.y2 (la20) 0.845 0.160 5.281 0.000
.y3 (la30) 0.045 0.168 0.267 0.789
Variances:
Estimate Std.Err z-value P(>|z|)
eta 1.000
.y1 (vps1) 0.910 0.168 5.409 0.000
.y2 (vps2) 1.345 0.231 5.835 0.000
.y3 (vps3) 2.033 0.272 7.487 0.000 13.4 Aufgabe 4
13.4.1 Output 1
Lösung: Modell tau parallel Modellgleichungen: \[ y1 = 0 + 1 \cdot \eta + \epsilon 1 \\ y2 = 0 + 1\cdot \eta + \epsilon 2 \\ y3 = 0 + 1\cdot \eta + \epsilon 3 \\ y4 = 0 + 1\cdot \eta + \epsilon 4 \\ \]
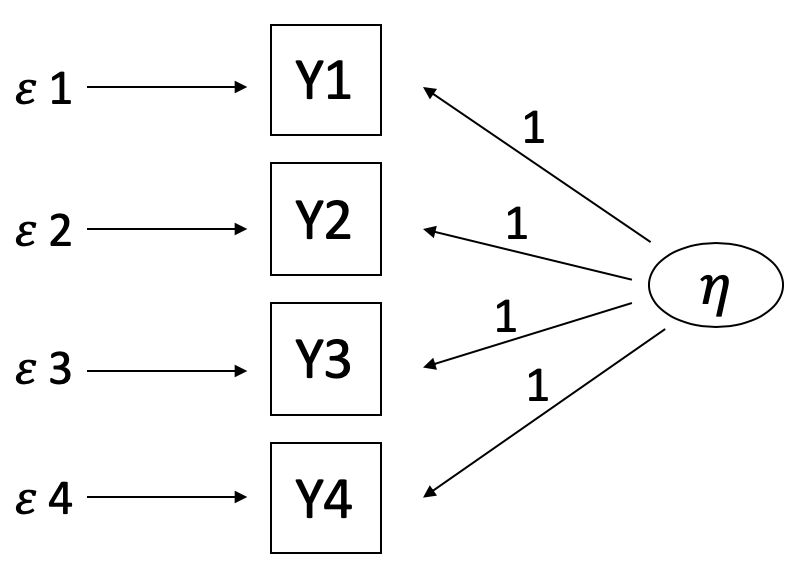
Figure 13.1: Übungsaufgabe 4 - Pfadmodell tau paralleles Messmodell
13.4.2 Output 2
Lösung: Essentiell tau äquivalentes Modell, Normierung la10 = 0 Modellgleichungen: \[ y1 = 0 + 1\cdot \eta + \epsilon 1 \\ y2 = -0.215 + 1\cdot \eta + \epsilon 2 \\ y3 = -0.075 + 1\cdot \eta + \epsilon 3 \\ y4 = -0.135 + 1\cdot \eta + \epsilon 4 \\ \]
Figure 13.2: Übungsaufgabe 4 - Pfadmodell essentiell tau äquivalentes Messmodell
13.4.3 Output 3
Lösung: Modell tau kongenerisch, Normierung E(eta)= 0 und Var(eta) = 1 Modellgleichungen: \[ y1 = 3.443 + 0.864\cdot \eta + \epsilon 1 \\ y2 = 3.460 + 0.004\cdot \eta + \epsilon 2 \\ y3 = 3.989 + 0.931\cdot \eta + \epsilon 3 \\ y4 = 2.994 + 0.432\cdot \eta + \epsilon 4 \\ y5 = 3.528 + 0.573\cdot \eta + \epsilon 5 \\ y6 = 5.051 + 0.785\cdot \eta + \epsilon 6 \\ y7 = 3.966 + 0.029\cdot \eta + \epsilon 7 \\ y8 = 3.267 + 1.051\cdot \eta + \epsilon 8 \\ \]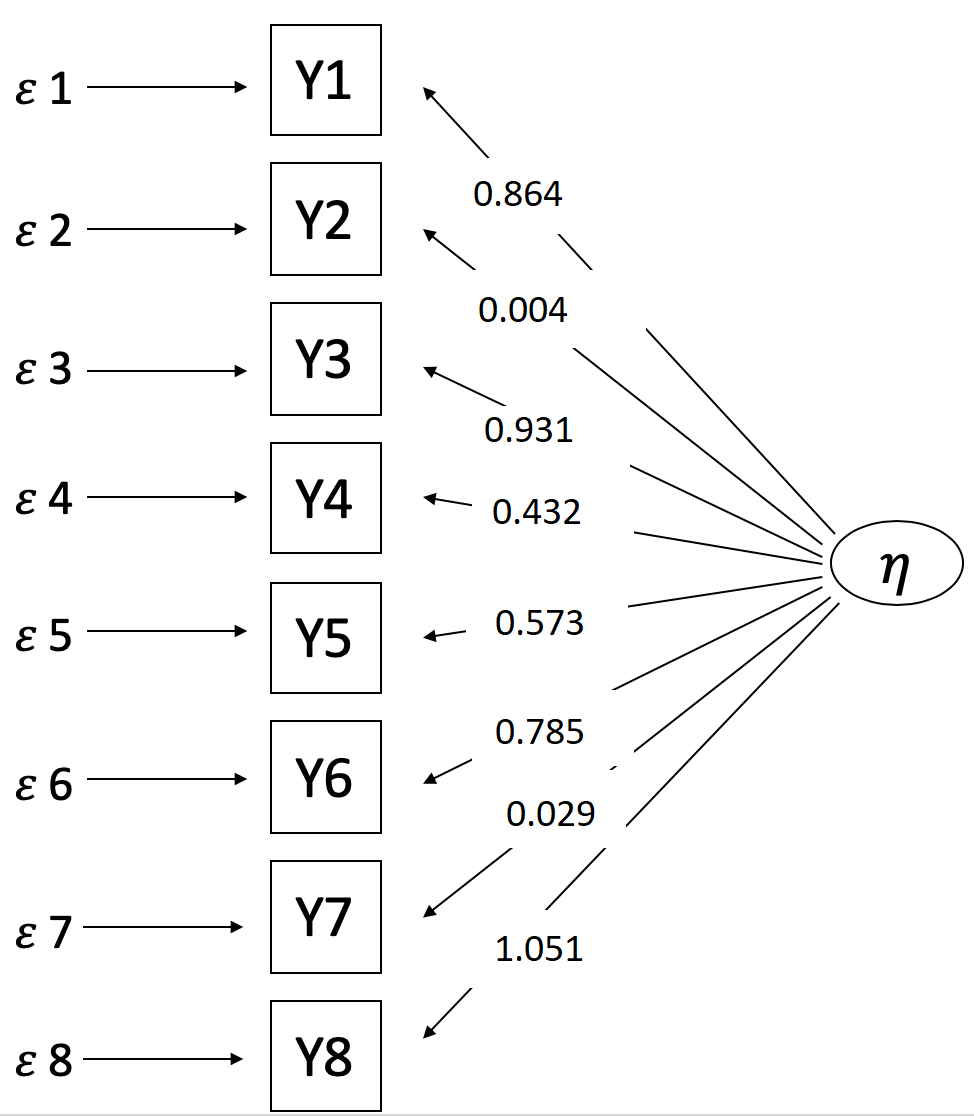
Figure 13.3: Übungsaufgabe 4 - Pfadmodell tau kongenerisches Messmodell
13.4.4 Output 4
Lösung: Modell tau kongenerisch, Normierung la10 = 0, la11 = 1 Modellgleichungen: \[ y1 = 0 + 1\cdot \eta + \epsilon 1 \\ y2 = -0.290 + 1.081\cdot \eta + \epsilon 2 \\ y3 = -0.226 + 1.050\cdot \eta + \epsilon 3 \\ y4 = -0.024 + 0.943\cdot \eta + \epsilon 4 \\ \]
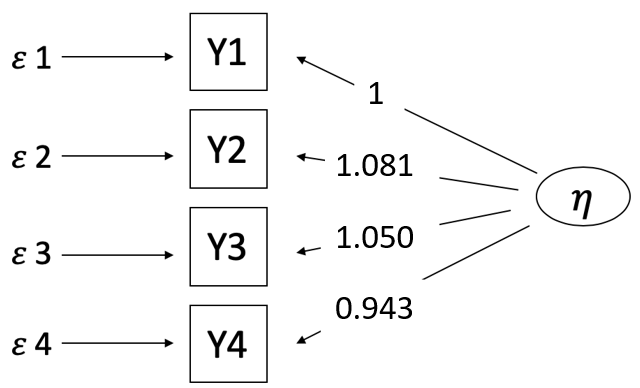
Figure 13.4: Übungsaufgabe 4 - Pfadmodell tau kongenerisches Messmodell